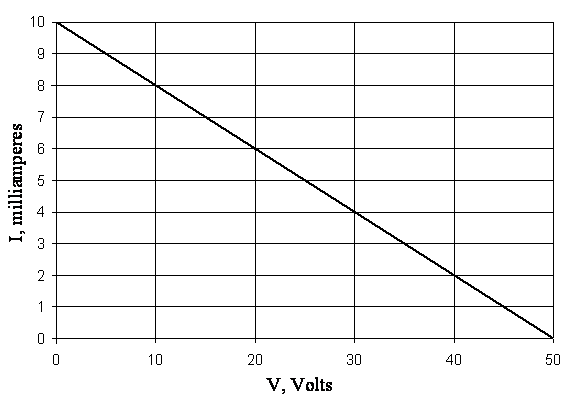Homework Given January
16, 2007
Due January23, 2007
These aren't homework problems per se; the Exercises are intended as a study aid for those reading the chapter. These are selected to make sure that the intended points stick with the student.
Live Links to the Exercises
Exercise 1.1
Plot the voltage-current curve of resistors of 1 k
, 5 k, and 20 k,
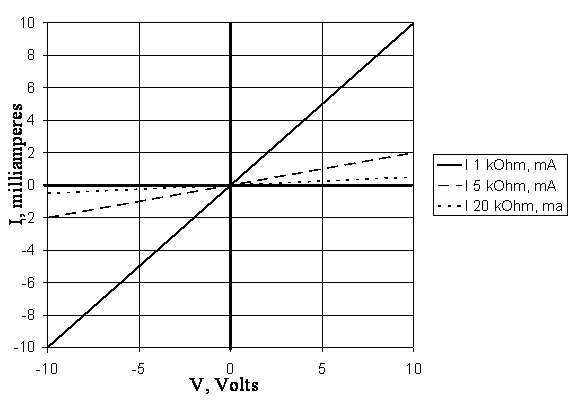
Exercise 1.5
Find the value of 
in Figure 1.5 if
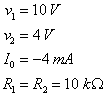
It's tempting to use a Norton equivalent of 
, 
, and 
, because that would result in two current sources in
parallel across two resistors in parallel, a very simple circuit to solve. However, the section is on superposition, so
we will solve it by superposition.
The component of 
from 
is
and the component 
from 
is identical,
.
The component of 
from 
is
.
The final value of 
is the sum of the
components from 
, 
, and 
,
.
For the values given in the problem statement, 
is
.
Exercise 1.12
Plot the v-I equation of the circuit of Figure 1.11 if the
value of 
is changed to
.
The figure is part of Example 1.3, which is a superposition example. To follow the intent of the exercise, we will solve it by superposition.
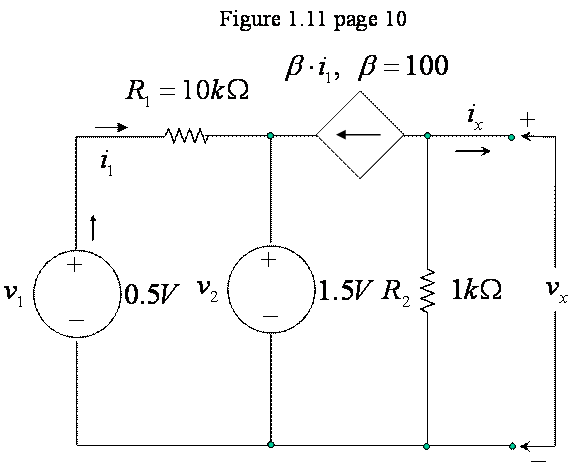
Note that the zig-zag transistor
model geometry of Figure 1.11 has been changed here to the more familiar ladder
configuration that we use for circuit analysis.
To plot the v-I characteristic
of 
and 
, we need to find the open circuit voltage and short circuit
current. In class, I solved this circuit
directly instead of using superposition as in Example 1.3, which is the context
for the figure. Here, we use
superposition.
The component of the open circuit voltage 
due to 
is found by finding 
and noting that the
controlled current source and 
form a Norton
equivalent across the terminals which 
is measured. This we have
The short circuit current is simply the controlled current
source current, negated because 
is positive out the
terminal, opposite the direction of the arrow in the controlled current source,
.
The voltage source 
drives current through
opposite than that of 
but its effect on the
controlled current source is otherwise identical, so we have
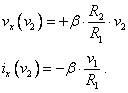
By superposition, the open circuit voltage is the sum of the
two voltages due to 
and 
, and the short circuit current is the sum of the currents
due to and ,
For the values given in the problem,
and, finally, the total open circuit voltage and short circuit current are
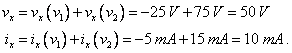
We plot the v-i curve from the open circuit voltage, when current is zero, and the short circuit current, when the voltage is zero, as a straight line between these points as below.
