Electronics I for ECE

Tuesday, January 18, 2007

Instructor:    James K Beard                                            RH 238A

Text:               Microelectronic Circuits and Devices, Mark N Horenstein

Time:              Tuesday, Thursday 10:50 AM to 12:05 PM       RH 239

Lab:                Friday, 8:00 AM to 10:40 AM                   RH 204/206

Web Site http://rowan.jkbeard.com, click on "Electronics I for ECE"

Assignment

Page 28, problems 1.1, 1.3, 1.7

Kirchoff's Laws as Linear Matrix Equations

Combining Kirchoff's voltage and current laws can give us a set of equations in the unknowns of node voltages in the familiar form

                                                                

where  is a square matrix of constants,  is a vector whose elements are the node voltages, and  is a vector which contains all the sources in the circuit.  The elements of the matrix A are the resistances and the controlled source multipliers.

Kirchoff's Voltage Law (KVL)

*      The sum of the voltage drops around a loop is zero.  "Conservation of voltage (energy)."

*      Don't forget voltages across current sources

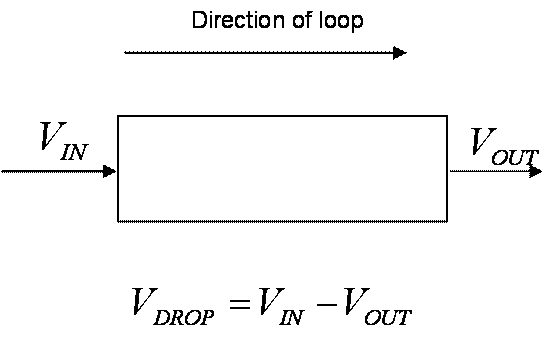
Figure 1.  Voltage Drop Across a Circuit Element

Kirchoff's Current Law (KCL)

*      The sum of the currents into a node is zero.  "Conservation of electrons (mass)."

*      Current into a node through each resistor is the voltage on the other side of each resistor divided by the resistance

*      Current out of a node is the voltage at that node times the sum of the reciprocals of all the resistors connected to the node

*      Add currents through sources

*      Current sources connected to the node

*      Currents through voltage sources connected to the node

*      Use Ohm’s Law to pose the currents through resistors in terms of the node voltages

Passive Sign Convention

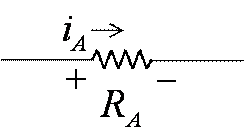
Figure 2.  Passive Sign Convention

*      Always mark one terminal of a passive component with a + sign.

*      Voltage is positive measured relative to that of the other terminal.

*      Current is positive going into the terminal marked with the + sign

Source Sign Convention

Figure 3.  Source Sign Convention
 

 

 

 

*      Voltage sources marked with + and – signs inside a circle or diamond

*      Current sources marked with an arrow inside a square, circle or diamond

*      Positive voltages and currents

*      Current out of a voltage source

*      Voltage out of a current source

Node Equations

There are usually fewer voltage nodes than independent currents in a circuit.  Therefore you can pose the KVL and KCL equations all in terms of the voltage nodes and get fewer equations.  However, the equations will be more complicated.

Mesh Equations

You can pose all the KVL and KCL equations in terms of the independent currents in the circuit.  This is simple to do, and consistent use of the sign conventions makes this process easy to do accurately.

Example

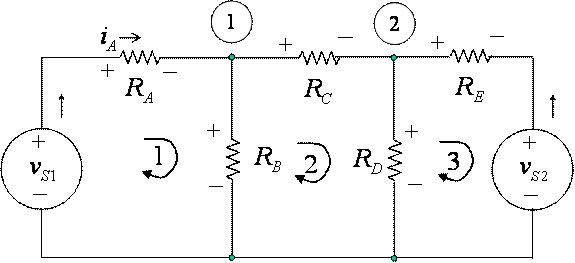
Figure 4 Circuit for Matrix Example

Loop 1

                                                   

Loop 2

                                                 

Loop 3

                                                   

Node 1

                                                            

Node 2

                                                            

Solution with the Mesh Equations

                            

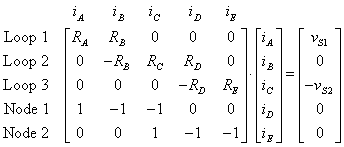
Solution with the Voltage Node Equations

The number of node voltages is equal to the number of nodes, which is equal to the number of node equations or KCL equations.  We get the VCL equations in terms of the node voltages by using Ohm's Law to write each of the currents in terms of the node voltages.

                                                             

 

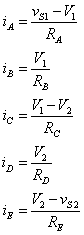
Then, use these currents with the current node (KCL) equations.

                                                  

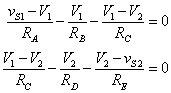
Rearrange to put the sources on the right hand side as before.

                                                 

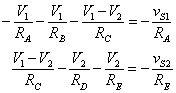
Now we can write the matrix form as we did with the mesh equations.

                      

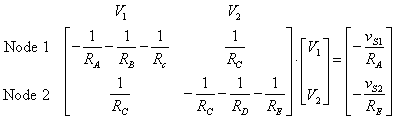
Note that the current into node 1 can be written by inspection from the circuit.  The current out of the node is the node voltage times the sum of the conductance, or the sum of the reciprocals of the resistances, connected to that node.  The current into that node due to the sources is the source times the conductance of the component between it and the node; on the right-hand-side of the equation this quantity is negated.  Thus the matrix form of the node voltage equation can be written directly from the circuit.

Resistor-Capacitor Circuits

The voltage  across an ideal capacitor is proportional to the charge on the capacitor  and inversely proportional to the capacitance .  The general equation is

                                                              .

Current is the rate at which charge traverses a circuit,

                                                            

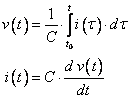
so Ohm's Law is replaced, for ideal capacitors, by a similar set of equations involving integrals and differentiation.

                                                       

Sine Wave Voltages across a Capacitor

Consider a sine wave of RMS voltage , at frequency ,

                                        

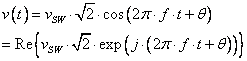
where the factor of  accounts for the ratio between peak and RMS amplitude, and  is a constant phase angle.  The current through a capacitor with this voltage across it is

                              

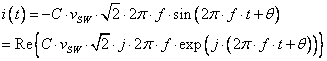
If we write the complex form of the current and voltage by using an appended "z" in the variable name, we can write the voltage and current law using a modified version of Ohm's Law.

                                                              

where the quantity that takes the place of resistance,  is the impedance of the capacitor,

                                                         .

Examine the circuit of Figure 5 below.  When the input voltage is a sine wave, the impedance concept allows the voltage divider equations to be used with the impedance concept to provide the amplitude of the output and its phase relative to the input.

 

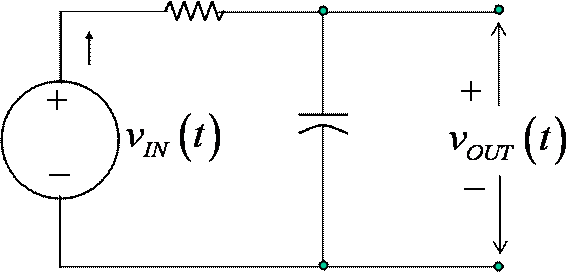
Figure 5 Simple Low-Pass RC Circuit with Source Voltage